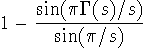| Verhehlen wollen wir aber auch nicht, daß bereits im 18. Jahrhundert Stimmen laut wurden, die gegen die Dominanz dieser Methode opponierten. Dieser Protest gegen die Beweisführung more geometrico etwa in der Kunst läßt sich an der literarischen Karriere eines mathematischen Topos durch mehr als zwei Jahrhunderte verfolgen. In der 1758 erschienenen Mathematikgeschichte von Montucia wird berichtet, der Mathematiker Robervat habe in Anschluß an ein Theaterstück (Iphigenia von Racine) gefragt: quŽest-ce que cela prouve? Diese Anekdote wurde seither in der Literatur immer wieder verwendet und mehrfach modifiziert.
Wir verzichten auf eine Wiedergabe der einzelnen Stationen dieser "Karriere" und machen einen Sprung zu Berthold Brecht, der an Nietzsches Ästhetik anknüpfte und auch darauf hinwies, daß es in verschiedenen Disziplinen unterschiedliche Auffassungen von Beweis gibt, die nicht miteinander kompatibel sind: "Angenommen, unser Mathematiker wäre vor ein Gedicht geführt worden, das den pythagoreischen Lehrsatz bewiesen hätte, würde er dann behauptet haben, dieses Gedicht beweise was? Vielleicht, aber wir hätten ihm vielleicht widersprochen, ebenso, wie wir ihm widersprachen, als er behauptete, die Iphigenie beweise nichts." |
Hier mündet die Diskussion in die umfassende Frage nach der Funktion des Beweises für die "Wahrheit von Aussagen". Wir werden später zu dieser Beweisproblematik zurückkehren.
Wenden wir uns nun nach der allgemeinen Faszination, die von den natürlichen Zahlen ausging, konkreten Fragestellungen zu, die nicht minder seit den Griechen Generationen von Gelehrten in ihren Bann gezogen haben und sich mit Eigenschaften der Primzahlen beschäftigen.
Jeder von uns weiß: Eine Primzahl ist ein natürliche Zahl, größer als 1, die durch keine weitere natürliche Zahl außer der 1 geteilt wird. Dies ist auch die Definition der Zahlentheoretiker, andere Mathematiker benutzen ab und zu andere Definitionen. So ist etwa für den Funktionentheoretiker eine Primzahl eine ganzzahlige Wurzel der analytischen Funktion
|