Verteilung der Primzahlen
In seinen "Elementen" beweist Euklid: "Es gibt unendlich viele Primzahlen". Seine Argumentation gilt bis heute als Paradebeispiel für einen eleganten Beweis, den wir alle in der Schule kennengelernt haben und den auch die, für die Mathematik ein Greuel war, verstehen konnten.
Das genannte Resultat läßt sich auch anders formulieren: Die Primzahlfunktion 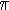 (x) die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen unendlich für x ® (x) die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen unendlich für x ® 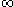 .
Gauß, für den die "Mathematik die Königin der Wissenschaften und die Zahlentheorie die Königin in der Mathematik" war, vermutete 1792 als Fünfzehnjähriger, daß der Quotient ( .
Gauß, für den die "Mathematik die Königin der Wissenschaften und die Zahlentheorie die Königin in der Mathematik" war, vermutete 1792 als Fünfzehnjähriger, daß der Quotient (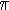 (x)log x)/x gegen 1 strebt für x ® (x)log x)/x gegen 1 strebt für x ®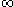 aber erst 1896 konnte dieses Resultat - bekannt als Primzahlsatz - von Hadamard und de la Vallée Poussin bewiesen werden. Die versprochene Unsterblichkeit wurde ihnen nicht zuteil - aber fast: Hadamard wurde 98 Jahre alt, de la Vallée Poussin 96.
Der Primzahlsatz läßt sich etwas vereinfacht auch statistisch interpretieren: Die Wahrscheinlichkeit für eine natürliche Zahl der Größenordnung x, eine Primzahl zu sein, ist ungefähr 1/ log x, d.h. in einem Intervall um x der Länge a liegen etwa a / log x Primzahlen. aber erst 1896 konnte dieses Resultat - bekannt als Primzahlsatz - von Hadamard und de la Vallée Poussin bewiesen werden. Die versprochene Unsterblichkeit wurde ihnen nicht zuteil - aber fast: Hadamard wurde 98 Jahre alt, de la Vallée Poussin 96.
Der Primzahlsatz läßt sich etwas vereinfacht auch statistisch interpretieren: Die Wahrscheinlichkeit für eine natürliche Zahl der Größenordnung x, eine Primzahl zu sein, ist ungefähr 1/ log x, d.h. in einem Intervall um x der Länge a liegen etwa a / log x Primzahlen. |
(damit dies statistisch sinnvoll ist, sollte a genügend groß, aber klein im Vergleich zu x sein). Jahrzehntelange Versuche, auf diesen Überlegungen aufbauend eine Wahrscheinlichkeitstheorie für die natürlichen Zahlen zu entwickeln, schlugen fehl, bis kürzlich durch die Einbettung der natürlichen Zahlen in ihre Stone-Cech-Kompaktifizierung eine derartige Theorie bewiesen werden konnte.
Kehren wir jedoch zu den obigen heuristischen Überlegungen zurück. Demzufolge ist die Wahrscheinlichkeit dafür, daß zwei zufällig (in der Umgebung von x) gewählte Zahlen beide Primzahlen sind, etwa 1 / (log x)2. Bezogen auf Primzahlzwillinge, d.h. Paare von Primzahlen, deren Differenz 2 ist, bedeutet dies, daß in Intervallen der genannten Art a / (log x)2 Primzahlzwillinge zu erwarten sind. (In Wirklichkeit etwas mehr, da die Tatsache, daß n prim ist, die Wahrscheinlichkeit für n+2, prim zu sein, verändert (z.B. ist n+2 dann sicher ungerade)). Heuristische Überlegungen führen zu Formeln über die Verteilung von Primzahlzwillingen, die überraschend gut mit numerischen Rechnungen übereinstimmen, überraschend deswegen, da noch nicht einmal bekannt ist, ob unendlich viele Primzahlzwillinge existieren. In diesem Zusammenhang sei erwähnt, daß wir kürzlich in Paderborn, vor allem in Zusammenarbeit mit Professor Antal Járai, das bisher größte bekannte Primzahlzwillingspaar finden konnten. |
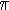 (x) die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen unendlich für x ®
(x) die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen unendlich für x ®