A prímszámok eloszlása
Euklidész "Elemek" címû mûvében bebizonyítja:
"Végtelen sok prímszám létezik". érvelése
máig is az elegáns bizonyítás mintapéldája.
Mindannyian ismerjük az iskolából és még
azok is megértették, akik számára a matematika
egyébként szörnyûség volt.
Az említett eredmény másképpen is fogalmazható:
A 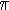 (x) prímszámfüggvény,
amely az x-nél kisebb prímszámok számát
adja meg, tart a végtelenhez, ha x-> (x) prímszámfüggvény,
amely az x-nél kisebb prímszámok számát
adja meg, tart a végtelenhez, ha x->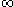 .
Gauss, akinek a matematika a tudományok királynôje,
s a számelmélet a matematika királynôje volt,
már 15 évesen azt sejtette, hogy a ( .
Gauss, akinek a matematika a tudományok királynôje,
s a számelmélet a matematika királynôje volt,
már 15 évesen azt sejtette, hogy a (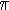 (x)log
x)/x hányados 1-hez tart, ha x® (x)log
x)/x hányados 1-hez tart, ha x®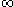 . De csak 1896-ban sikerült ezt a - prímszámtételként
közismert - eredményt Hadamard-nak [4] és de la Vallée
Poussin-nak [10] bebizonyítani. Az ígért hallhatatlanság
nem jutott nekik osztályrészül, csak majdnem: Hadamard
98, de la Vallée Poussin 96 évig élt.
Kicsit leegyszerûsítve a prímszámtétel
statisztikusan is interpretálható: Annak a valószínûsége,
hogy egy x nagyságrendû természetes szám prím
legyen, körülbelül 1/log x, azaz egy x körüli
a hosszúságú intervallumban közelítôleg
a/log x prímszám van.
. De csak 1896-ban sikerült ezt a - prímszámtételként
közismert - eredményt Hadamard-nak [4] és de la Vallée
Poussin-nak [10] bebizonyítani. Az ígért hallhatatlanság
nem jutott nekik osztályrészül, csak majdnem: Hadamard
98, de la Vallée Poussin 96 évig élt.
Kicsit leegyszerûsítve a prímszámtétel
statisztikusan is interpretálható: Annak a valószínûsége,
hogy egy x nagyságrendû természetes szám prím
legyen, körülbelül 1/log x, azaz egy x körüli
a hosszúságú intervallumban közelítôleg
a/log x prímszám van. |
(Ahhoz, hogy ez statisztikailag értelmes legyen,
az a-nak elég nagynak, de x-hez képest elég kicsinynek
kell lenni.) Az évtizedeken keresztül tartó ismételt
próbálkozások, hogy a természetes számokra
egy - ezeken a megfontolásokon alapuló - valószínûségelméletet
dolgozzanak ki, sorra kudarcba fulladtak, mígnem röviddel ezelôtt
a természetes számoknak a Stone-Cech kompaktifikációjukba
történô beágyazása révén
egy ilyen elmélet bizonyítást nyerhetett.
Térjünk most mégis vissza a fenti heurisztikus fejtegetésekhez.
Ezek szerint annak a valószínûsége, hogy az
x környezetében választott két szám mindegyike
prím, Úgy 1/(log x)2 körül van.Ikerprímekre,
azaz olyan prímszám párokra vonatkoztatva, amelyek
különbsége 2, ez azt jelenti, hogy az említett
tulajdonságú intervallumban a/(log x)2 ikerpím
várható. (Igazából egy kicsit több, mert
az a tény, hogy x prím, megváltoztatja annak a valószínûségét,
hogy x+2 is prím legyen. Pl. x+2 biztosan páratlan.) Heurisztikus
megfontolások az ikerprímek eloszlásával kapcsolatosan
olyan formulákhoz vezetnek, amelyek meglepô módon megegyeznek
a numerikus számításokkal. Meglepô ez azért,
mert még az sem ismert, vajon létezik-e végtelen sok
ikerprím. Ebben az összefüggésben hadd említsük
meg, hogy nemrég Paderbornban Járai Antal professzorral együttmûködve
sikerült a ma ismert legnagyobb ikerprím-párt megtalálni
[5]. |
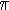 (x) prímszámfüggvény,
amely az x-nél kisebb prímszámok számát
adja meg, tart a végtelenhez, ha x->
(x) prímszámfüggvény,
amely az x-nél kisebb prímszámok számát
adja meg, tart a végtelenhez, ha x->