ForschungZahlentheorieEs ist nicht unser Bestreben, hier an dieser Stelle über die Vielfalt der Forschungsaktivitäten in der AG Zahlentheorie zu berichten – es würde den vorgegebenen Rahmen sprengen, andererseits geben die Schautafeln im Bauteil D 3 einen ausreichenden Überblick. Stattdessen wollen wir einige "Hintergrundinformationen" zu unserer Suche nach großen Primzahlzwillingen geben. Dabei könnte das Motto des Themenkreises lauten: "Auch Mathematiker gehen zuweilen auf Rekordjagd", wie es die Wochenzeitschrift DIE ZEIT am 17.5.1996 in ihrem Bericht über unseren Primzahlzwillingsrekord formuliert hat. Für uns war dieser "sportliche Grund" aber nicht alleine maßgebend. Primzahlen und PrimzahlzwillingeAllen ist bekannt: Eine Primzahl ist eine natürliche Zahl größer als 1, die durch keine weitere natürliche Zahl außer der 1 geteilt wird. Dies ist auch die Definition der Zahlentheoretiker, andere Mathematiker benutzen ab und zu andere Definitionen. So ist etwa für den Funktionentheoretiker eine Primzahl die ganzzahlige Wurzel der analytischen Funktion
für den Algebraiker ist sie "die Charakteristik eines endlichen Körpers" oder "eine nicht-archimedische Bewertung", der Kombinatoriker definiert die Primzahlen induktiv durch die Rekursion
([x]: ganzzahliger Teil von x) und der Logiker als die positiven Werte des Polynoms F(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v,w, x, y, z) = Wir begnügen uns mit der erstgenannten Definition. Über die Verteilung der Primzahlen haben wir bereits seit Euklid erste Informationen: Es gibt unendlich viele Primzahlen.
Seine Argumentation gilt bis heute als Paradebeispiel für einen eleganten mathematischen Beweis, den wir alle in der Schule kennengelernt haben und den
auch die, für die Mathematik ein Horror war, verstehen konnten. Das genannte Resultat läßt sich auch anders formulieren: Die Primzahlenfunktion
ist, aber erst 1896 konnte dieses Resultat bewiesen werden. Dieser sogenannte Primzahlsatz läßt sich auch statistisch
interpretieren: Die Wahrscheinlichkeit für eine natürliche Zahl der Größenordnung x, eine Primzahl zu sein, ist ungefähr
für die Anzahl der Primzahlzwillinge im Intervall [x, x+a]. Numerische Rechnungen führen zu überraschenden Übereinstimmungen mit der Theorie, überraschend insbesondere für Primzahlzwillinge, da noch nicht einmal bekannt ist, ob unendlich viele Primzahlzwillinge existieren.
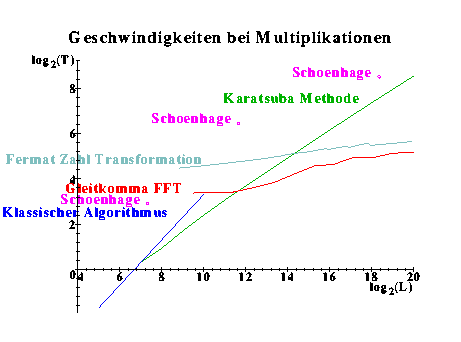
Suche nach großen PrimzahlzwillingenIn einem Projekt "Massiv parallele Rechner in der Computational Number Theory" entwickelten und implementierten wir Algorithmen für das schnelle Rechnen (z.B. Multiplikation) für sehr große Zahlen mit bis zu einer Milliarde Binärstellen. Bezüglich der erreichten Rechengeschwindigkeit, etwa der Multiplikation, haben wir einige Vergleiche in der folgenden Abbildung angegeben.
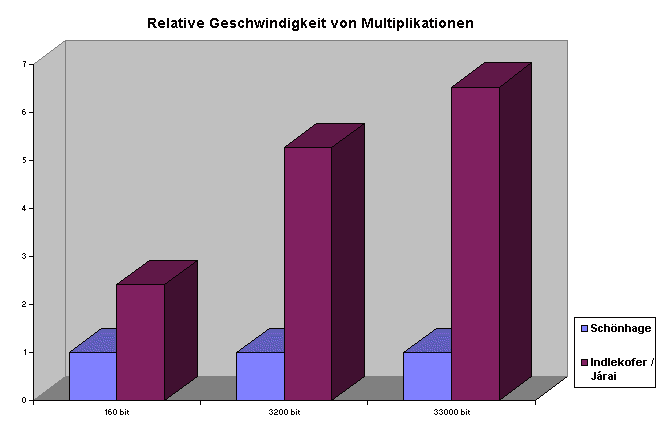
Die klassische Schulmethode ist nur für Zahlen mit weniger als einigen hundert Binärstellen optimal (jeweils abhängig von der Hardware). Weit besser ist – bis zu zehntausend Binärstellen – die einfache rekursive Methode von Karatsuba. Für noch größere Zahlen sind komplexere Methoden, die auf der Fast-Fourier-Transformation (FFT) beruhen, den anderen Verfahren überlegen. Eine Möglichkeit ist die Gleitkomma FFT, eine andere die schnelle Multiplikation in Restklassenringen auch die modulo Fermatzahlen. Welche schneller ist, hängt jeweils von der Hardware ab. Zum direkten Vergleich mit den von Schönhage A. (Schönhage et. al. Fast algorithms: a multitape turing machine implementation. BI-Wiss.-Verlag 1994) veröffentlichten Zeiten von 30 µs, 7ms, 3s für die Multiplikationen von 160 bit-, 3200 bit- bzw. 332224 bit-Zahlen sind unsere Zeiten 12 µs, 1.3 ms bzw. 0.46 s, wobei alle Resultate jeweils auf einer SUN S10 40 MHz erzielt wurden.
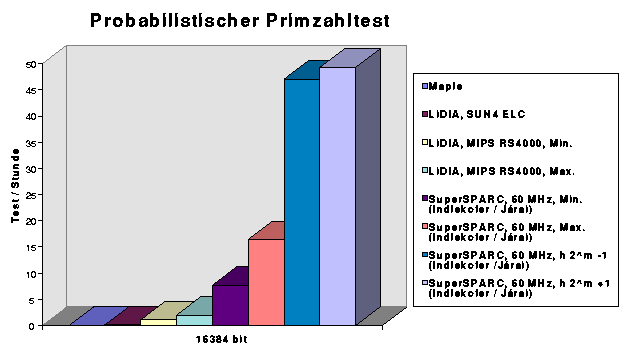
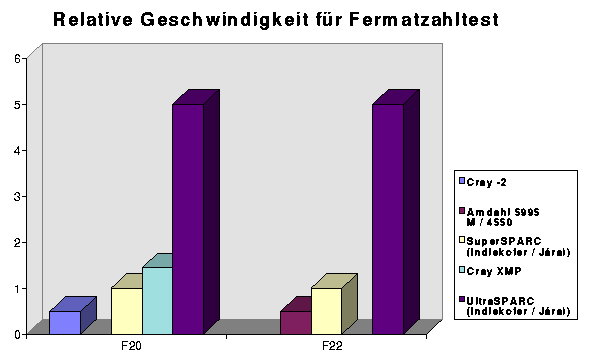
Die Geschwindigkeit der Multiplikationen ist der "kritische" und ausschlaggebende Teil in vielen Bereichen der "Computational Number Theory" oder auch der numerischen Mathematik. Denn nicht nur die Division kann auf die Multiplikation zurückgeführt werden (indem man die Newton-Approximation zur Berechnung der Reziproken benutzt), sondern auch die Multiplikation von Polynomen, die Berechnung algebraischer und anderer Funktionen und weiterer, darauf basierender Operationen. So ist die Multiplikation beispielsweise grundlegender Bestandteil unserer Programme für probabilistische Primzahltests und des Primzahltests für Fermatzahlen Fn = 22n+ 1. Die beiden folgenden Diagramme vermitteln einen guten Eindruck von der erreichten Geschwindigkeit, insbesondere gegenüber Supercomputern.
Kehren wir zurück zur eingangs erwähnten Rekordjagd nach großen Primzahlzwillingen. Das zugrundeliegende Such-Prinzip läßt sich kurz wie folgt beschreiben.
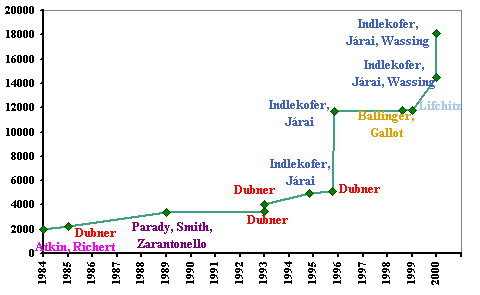
Primzahlzwillingsrekorde
Literatur
| ||||||||||||||||||||||||||||||||||||||||||||
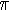 (x), die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen
(x), die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen  . Gauss vermutete bereits als Fünfzehnjähriger (1792), daß
. Gauss vermutete bereits als Fünfzehnjähriger (1792), daß