ForschungPrimzahltestPrimzahltest durch ProbedivisionDas Verfahren beruht auf der Tatsache, daß eine natürliche Zahl n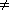 1, die außer 1 keinen Teiler d
1, die außer 1 keinen Teiler d n1/2
besitzt, prim ist; ist nämlich n = d1d2
mit
d1,d2 n1/2
besitzt, prim ist; ist nämlich n = d1d2
mit
d1,d2 N,
so ist d1 N,
so ist d1 n1/2
oder
d2 n1/2
oder
d2 n1/2. Um
festzustellen, ob eine Zahl n Primzahl ist, braucht man nur für
alle Primzahlen
p n1/2. Um
festzustellen, ob eine Zahl n Primzahl ist, braucht man nur für
alle Primzahlen
p n1/2 zu
testen, ob sie n teilen. n1/2 zu
testen, ob sie n teilen.
Der Aufwand für diesen Primzahltest wird gegeben durch die Anzahl.
der Probedivisionen, die notwendig sind für den Beweis, daß n eine Primzahl ist. Beachtet man die bekannten Abschätzungen von J. Rosser und L. Schoenfeld
Die Probedivision ist ein exakter (oder terministischer) Primzahltest, d.h. ein Verfahren, das beweist, daß eine Zahl n prim ist. Daneben gibt es eine Anzahl von Verfahren, die feststellen können, daß eine Zahl n mit hoher Wahrscheinlichkeit prim ist. Solche Verfahren nennt man probabilistische Primzahltests. Ein derartiger Test ist der Fermat Test.Er beruht auf dem sogenannten,,Kleinen Satz von Fermat". Ist n eine Primzahl, so gilt für alle zu n teilerfremden Zahlen a an-1
Mit diesem Satz läßt sich feststellen, ob eine Zahl n
zusammengesetzt ist. Man wählt eine Zahl a, (1 < a
< n), und berechnet
an-1 mod n.
Ist dies Wir nennen eine zusammengesetzte Zahl n eine Pseudoprimzahl zur Basis a, falls an-1
gilt. Ist n eine Pseudoprimzahl zur Basis a für allea, die teilerfremd zu n sind, dann heißt nCarmichael-Zahl. Es gibt unendlich viele Carmichael-Zahlen. (Ein Beispiel für eine Carmichael-Zahl ist n = 561.) Aus diesem Grund ist der Fermat-Test für die Praxis nicht geeignet. Anders verhält es sich bei den folgenden Tests. Miller Test.Grundlage hierfür ist die folgende Verschärfung des kleinen Satzes von Fermat.Satz (Miller). Schreiben wir eine ungerade ganze Zahln > 1 in der Formn-1 = 2eu mit ungeradem u, so sind die folgenden Aussagen äquivalent
Miller-Rabin-TestIst n eine zusammengesetzte Zahl und findet man ein zu n teilerfremdes a, für das weder (1) noch (2) für ein k mit 0 k k e-1
gilt, so ist a nicht prim. Eine solche Zahl nennt man nach Rabin
einen
Zeugen gegen die Primheit von n. Eine Abschätzung
der Anzahl dieser Zeugen geht auf Rabin zurück, und eine einfache
Version seines Resultates ist enthalten in folgendem e-1
gilt, so ist a nicht prim. Eine solche Zahl nennt man nach Rabin
einen
Zeugen gegen die Primheit von n. Eine Abschätzung
der Anzahl dieser Zeugen geht auf Rabin zurück, und eine einfache
Version seines Resultates ist enthalten in folgendem
Satz (Rabin). Sei n > 3 eine ungerade zusammengesetzte
Zahl, Dann ist die Anzahl dera Zur Anwendung des Miller-Rabin-Tests auf eine ungerade Zahl n
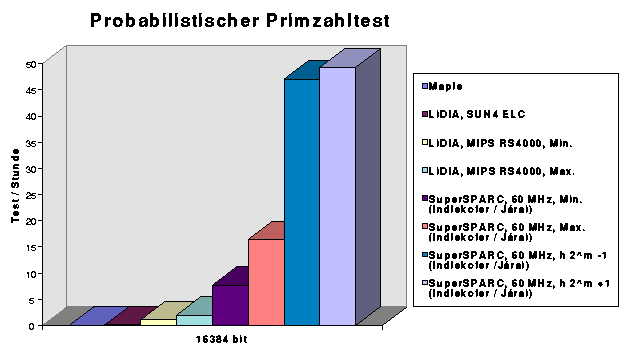
wählt man eine beliebige Zahl a mit 2 Wir haben den Miller-Rabin-Test implementiert. Er benötigt für
einen Test bei einer Zahl n den Größe 10100
ca. 0,062 Sekunden (bei 1010000 ca. 3526 Sekunden) auf einem
Super-SPARC-Prozessor mit 40MHz.
Literatur [1.] K.-H. Indlekofer, A. Járai, Largest known twin primes, Math. Comp. 65(1996), 427-428. MR 96d:11009 |
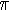 (n1/2) := #{p
(n1/2) := #{p 1 mod n
1 mod n